今天本来计划了总共六道题的,但现在我想把侧重点放在stm32的学习上,把刷题的优先级往后排一排。
2312. 卖木头块 , 54. 螺旋矩阵 , 48. 旋转图像
2312.卖木头块:
给你两个整数 m 和 n ,分别表示一块矩形木块的高和宽。同时给你一个二维整数数组 prices ,其中 prices[i] = [hi, wi, pricei] 表示你可以以 pricei 元的价格卖一块高为 hi 宽为 wi 的矩形木块。
每一次操作中,你必须按下述方式之一执行切割操作,以得到两块更小的矩形木块:
-
- 沿垂直方向按高度 完全 切割木块,或
- 沿水平方向按宽度 完全 切割木块
在将一块木块切成若干小木块后,你可以根据 prices 卖木块。你可以卖多块同样尺寸的木块。你不需要将所有小木块都卖出去。你 不能 旋转切好后木块的高和宽。
请你返回切割一块大小为 m x n 的木块后,能得到的 最多 钱数。
注意你可以切割木块任意次。
示例:
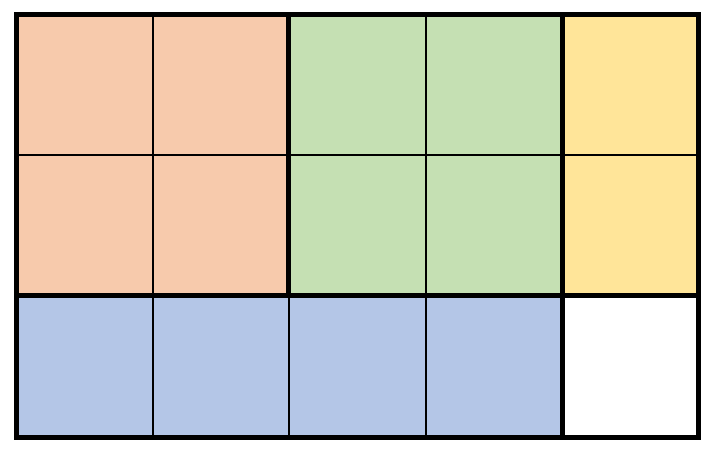
输入:m = 3, n = 5, prices = [[1,4,2],[2,2,7],[2,1,3]] 输出:19 解释:上图展示了一个可行的方案。包括: - 2 块 2 x 2 的小木块,售出 2 * 7 = 14 元。 - 1 块 2 x 1 的小木块,售出 1 * 3 = 3 元。 - 1 块 1 x 4 的小木块,售出 1 * 2 = 2 元。 总共售出 14 + 3 + 2 = 19 元。 19 元是最多能得到的钱数。
本题是比较新型的动态规划题目,我给dp数组的定义是dp[i][j]表示高为i,宽为j的木块能卖的最多钱数。
分为了高和宽这两个维度,我们就需要分别从高和宽两个维度去切割木头寻找钱数最大化的组合,所以我们遍历一个木块大小的时候,就需要切割其寻找dp[i][j]与切割点在k时所能卖的钱数dp[i][k] + dp[i][j – k],要取这两个数的最大值,这是切割宽度的,我们还要再遍历切割高度。
dp[i][j]与dp[i – k][j]中取最大值,再在这两个取好的最大值中再取最大值就是高i,宽j木块能卖的最大钱数了。
class Solution {
public:
long long sellingWood(int m, int n, vector<vector<int>>& prices) {
vector<vector<int>> pr(m + 1, vector<int>(n + 1));
for (auto &p : prices){
pr[p[0]][p[1]] = p[2];//得到木块高宽对应的价钱
}
vector<vector<long long>> f(m + 1, vector<long long>(n + 1));
for (int i = 1; i <= m; i++){
for (int j = 1; j <= n; j++){
f[i][j] = pr[i][j];//如果有对应的价钱就能加入到dp数组中用于后面最大值比较中。
for (int k = 1; k < j; k++) f[i][j] = max(f[i][j], f[i][k] + f[i][j - k]);//切割宽
for (int k = 1; k < i; k++) f[i][j] = max(f[i][j], f[k][j] + f[i - k][j]);//切割高
}
}
return f[m][n];
}
};54.螺旋矩阵 题目描述:
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]
本题和我之前做过的螺旋矩阵II是兄弟题目。本题主要还是要注意上下左右这四个边界参数的调整,比如从左到右遍历完第一行之后,上边界就要加一往下走了,从上到下遍历完最后一列时,右边界就需要减一往左走了,再从右到左遍历最后一行时,下边界就需要减一往上走了,再从下往上遍历第一列时,就需要将左边界加一往右走了。其实这些就是这道题的主体代码了,剩下的就是判断边界参数的重叠情况了。如果发现重叠时就说明我们的遍历已经可以结束了。
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
if (matrix.empty()) return {};
int l = 0, r = matrix[0].size() - 1, t = 0, b = matrix.size() - 1;
vector<int> result;
while (true){
for (int i = l; i <= r; i++) result.push_back(matrix[t][i]);//从左到右遍历上边界
if (++t > b) break;//上边界往下走,并且判断上边界是否与下边界重叠
for (int i = t; i <= b; i++) result.push_back(matrix[i][r]);//从上到下遍历右边界
if (l > --r) break;//右边界往左走,并判断右边界是否与左边界重叠
for (int i = r; i >= l; i--) result.push_back(matrix[b][i]);
if (t > --b) break;
for (int i = b; i >= t; i--) result.push_back(matrix[i][l]);
if (++l > r) break;
}
return result;
}
};48.旋转图像 题目描述:
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
本题要求要在原地修改,不能够再创建其他数组来存储中间过程的数。在原数组中操作我们在数据移动的时候,肯定会有数据丢失的情况,比如我们先将数组的四角进行旋转,左上角的值赋给右上角,右上角的再赋给右下角,右下角再赋值给左上角。这段操作中,我们从左下角开始,左下角值赋给左上角,右下角值赋给左下角,右上角的值赋给右下角,这时我们会发现左上角和左下角的值都是左下角的值,而左上角的值丢失了,所以我们需要一开始先把左上角的值存起来,最后再将其赋回给左上角。
我们需要一个数的位置就能够通过推测得到其作为左上角,对应的右上角,右下角,左下角这三个其他的位置,所以我们只需要遍历整个数组的左上角即可。遍历矩阵长宽各一半就行了。

class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
for (int i = 0; i < n / 2; i++){
for (int j = 0; j < (n + 1) / 2; j++){//选择遍历到(n + 1) / 2是为了防止矩阵边长为奇数
int tmp = matrix[i][j];
matrix[i][j] = matrix[n - 1 - j][i];
matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
matrix[j][n - 1 - i] = tmp;
}
}
}
};当矩阵的行列数为奇数时,中心元素是唯一的,需要在旋转操作中特殊处理。将中心点包括在要遍历的范围中可以确保中心元素也参与到了旋转操作中,从而保证了整个矩阵的正确旋转。
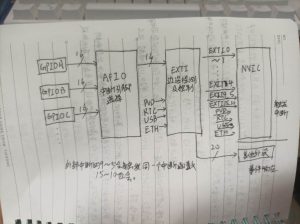
今天学习了中断的知识,之前学过51单片机所以还是比较熟悉的,但还是做了很多笔记,我觉得对专业一点的术语表达还是要多熟悉一些。


今日推荐歌曲:蓮の花——sakanaction(点击左下角倒数第八首歌即可收听)
