今天是训练营的最后一天了,只有一题,顺带做了一下每日一题。
84. 柱状图中最大的矩形 , 2673. 使二叉树所有路径值相等的最小代价
84, 柱状图中的最大矩形 题目描述:
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例:

输入:heights = [2,1,5,6,2,3] 输出:10 解释:最大的矩形为图中红色区域,面积为 10
本题和接雨水那道题十分相像, 可以说是遥相呼应, 接雨水是寻找凹槽, 往左往右寻找第一个遇到的比自身大的数, 本题是寻找高处, 往左往右寻找第一个比自身小的数。 暴力解法中本题同样也可以使用预处理的方法找出每个矩形左右各自第一个遇到的目标元素的下标。
暴力解法:
具体思路还是预先处理好每个矩形各自左右两边的下标情况:
vector<int> minLheight(heights.size());
vector<int> minRheight(heights.size());
int size = heights.size();
minLheight[0] = -1;
for (int i = 1; i < heights.size(); i++){
int t = i - 1;
while(t >= 0 && heights[t] >= heights[i]) t = minLheight[t];
minLheight[i] = t;
}
minRheight[size - 1] = size;
for (int i = size - 2; i >= 0; i--){
int t = i + 1;
while (t < size && heights[t] >= heights[i]) t = minRheight[t];
minRheight[i] = t;
}但其中判断条就稍微有点绕,因为最左边的矩形没有再往左的元素了,为了使判断条件while不陷入死循环加入t >= 0。如果说前一个元素大于当前遍历元素,说明前一个元素可以沿用本元素的高度,也就是说可以在前一个元素中取到和本元素同样的高度的矩形来组合。把minLheight[0]赋值为-1其实就是想表达,本元素到下标-1之间都可以沿用本元素的高度,使高度和宽度相乘来得到矩形面积。同理minRheight数组也能得到右边的目标下标。minRheight与minLheight相减即可得每个矩形向左向右能够沿用到的自身的宽度,再乘以自身高度即可得出以本元素的高度为高的最大面积。
最后用一个result记录出每段矩形得到的最大面积中的最大即可。
int result = 0;
for (int i = 0; i < size; i++){
int sum = heights[i] * (minRheight[i] - minLheight[i] - 1);
result = result > sum ? result : sum;
}
return result;
单调栈:
单调栈的做法与接雨水的就差不太多,主要就是把单调递增栈换成了单调递减栈。如果当前元素大于栈顶元素就可将其放入栈中,即可形成单调递减的栈。同样的,如果相同的话既可以放入栈中也可选择不放入。
if (heights[i] > heights[st.top()]) st.push(i);else if (heights[i] == heights[st.top()]){st.pop();st.push(i);}
如果当前遍历元素小于栈顶元素,说明我们找到了以栈顶元素的高度为高能组成的最大矩形面积的右边界,其左边界就是栈顶元素的下一个元素。
else{
while(!st.empty() && heights[i] < heights[st.top()]){
int mid = heights[st.top()];
st.pop();
if (!st.empty()){
int left = st.top();
int right = i;
int w = right - left - 1;
int sum = w * mid;
result = result > sum ? result : sum;
}
}
st.push(i);
}需要注意的是如果遇到了矩形数组本身就是单调递增的,那么这个数组就不会触发单调栈的计算程序。所以我们需要在矩形数组的两边都加上0
heights.insert(heights.begin(), 0);
heights.push_back(0);如果数组本身就是单调递增的,加入到栈中就会变成单调递减的,此时如果再来一个当前元素0来与栈顶元素进行比较,那么就可以一直触发单调栈的计算机制,直到最后一个元素弹出。
如果首个元素加入到栈后,第二个元素就小于栈顶元素,但取得栈顶元素的值作为高后弹出,再想去栈顶元素的值作为最大矩形面积的左边界时就已经没有元素了,此时如果在矩形数组最前面加上一个元素0的话,就可以解决这样的问题了。
2673. 使二叉树所有路径值相等的最小代价 题目描述:
给你一个整数 n 表示一棵 满二叉树 里面节点的数目,节点编号从 1 到 n 。根节点编号为 1 ,树中每个非叶子节点 i 都有两个孩子,分别是左孩子 2 * i 和右孩子 2 * i + 1 。
树中每个节点都有一个值,用下标从 0 开始、长度为 n 的整数数组 cost 表示,其中 cost[i] 是第 i + 1 个节点的值。每次操作,你可以将树中 任意 节点的值 增加 1 。你可以执行操作 任意 次。
你的目标是让根到每一个 叶子结点 的路径值相等。请你返回 最少 需要执行增加操作多少次。
示例:
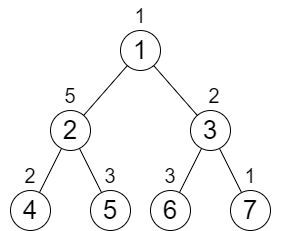
输入:n = 7, cost = [1,5,2,2,3,3,1] 输出:6 解释:我们执行以下的增加操作: - 将节点 4 的值增加一次。 - 将节点 3 的值增加三次。 - 将节点 7 的值增加两次。 从根到叶子的每一条路径值都为 9 。 总共增加次数为 1 + 3 + 2 = 6 。 这是最小的答案。
题目给出的是慢二叉树,也就是除了叶子结点以外的所有节点都会有两个孩子,此时要使所有路径值相等,最小的代价应该是从叶子结点入手更改数值,因为同一条路径到同父的两个叶子结点时,只要增加两个叶子结点中小的那个值直到两叶子值相等即可达到这两条路径的值相等的目的。
此时这两条的路径值已经相等,此时可以将其中一个孩子的值与父节点的值相加,再将两个孩子节点砍掉。同样的,将该父节点假设为一个其父节点(即被砍掉的两个孩子节点的祖父节点)的左孩子,同样的操作也可以在这个祖父节点的右孩子身上进行(即取两个孩子中值较大的那个与自己的值相加,然后将两个孩子砍掉,使自己变成叶子结点),这样两个原本的中间节点就变成了叶子结点,再重复前面砍孩子的操作,就可以使得两条路径的值相等,并且以最小的代价达成。
class Solution {
public:
int minIncrements(int n, vector<int>& cost) {
int ans = 0;
for (int i = n / 2; i > 0; i--){
ans += abs(cost[i * 2] - cost[i * 2 - 1]);
cost[i - 1] += max(cost[i * 2], cost[i * 2 - 1]);
}
return ans;
}
};因为是满二叉树,树的节点数量除以二之后其实就是除了叶子结点以外的节点的个数,从这些中间节点开始补全叶子结点使两个叶子相等再将其中一个孩子的数值加入自身这个中间节点的值中,再将孩子砍掉使自身作为叶子结点来进行同样的操作,但实机操作起来,并不需要砍掉叶子结点,只是单纯的把值加入中间节点,并再接下来的循环中会像前面的操作一样来操作这个中间节点,也就是遍历到这个中间节点的父节点的时候。
今天已经是代码随想录算法训练营的最后一天了,感觉真的过得很快。一直觉得这种时间快速流速的感觉一般只会在虚度时光之后出现。但这个寒假我觉得是我从出生以来学习时间最多的寒假了,也有可能是因为这是我放过最长的寒假(12月22号到3月4号😪😪),庆幸自己报名了这个训练营,不然这么长的寒假可能就完全浪费掉了。
虽然现在刷完了这60多天的代码应该有所蜕变,但是焦虑的心情却更加浓烈了,当初就是因为焦虑报名的,没想到确确实实认真学完后却更加焦虑了🤔,可能是因为前面没有写博客日志,因为我前面没有意识到写博客的重要性,希望现在开始还来得及吧。但主要焦虑的原因还是,最近加入代码随想录的知识星球后,感觉自己还是不太适合做c++算法开发这些工作。因为看到好多问问题的都是研究生出来就业找这些工作,感觉他们学历更高的找这些工作都这么有难度了,像我这种没参加过竞赛,没做过什么项目的本科生真找不到什么岗位,而且没多少时间了,就剩半年多就要开始秋招了,感觉这么短时间内也准备不出什么。最后还是想找和自己专业(物联网工程)比较相关的嵌入式开发之类的岗位。已经下单了stm32单片机,下定决心这半年搓几个项目出来,希望到时后秋招可以找到工作吧。
但这两个月的学习还是让我改变了很多的,之前总是静不下心来学,看到长串的代码就不想学,现在每天不刷两道力扣题就浑身难受🤪。对于数据结构的理解也更高了,对于以后单片机的学习也有一定的帮助。而且养成了写博客的习惯(虽然是最后这两天才开始😅),但如果能一直坚持下去的话,估计还是不错的,能锻炼表达能力的同时还能够锻炼打字能力💪💪💪。
最后,别太焦虑了,开心点吧😘
今日推荐歌曲 お気楽KING——ピーナッツくん/ぽんぽこ(点击左下角歌单,倒数第三首)
