今天带来的题目比较多,是这几天的每日一题:
834. 树中距离之和 , 2368. 受限条件下可到达节点的数目 , 2581. 统计可能的树根数目 , 2369. 检查数组是否存在有效划分
834 树中距离之和 题目描述:
给定一个无向、连通的树。树中有 n 个标记为 0...n-1 的节点以及 n-1 条边 。
给定整数 n 和数组 edges , edges[i] = [ai, bi]表示树中的节点 ai 和 bi 之间有一条边。
返回长度为 n 的数组 answer ,其中 answer[i] 是树中第 i 个节点与所有其他节点之间的距离之和。
示例:

输入: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]] 输出: [8,12,6,10,10,10] 解释: 树如图所示。 我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5) 也就是 1 + 1 + 2 + 2 + 2 = 8。 因此,answer[0] = 8,以此类推。
刚开始看到这道题还是很懵的,因为是第一次遇到这种换根dp的题目,根本没有思路,题都不怎么看的懂。
其实就是给出edges二维数组,数组中表示的是树中每两个相邻节点之间的连成的边,点与点之间的边知道了,但不知道哪个节点是根节点,要求给出每个节点到除自己之外的节点的距离的总和。
暴力的解法就是dfs(深度优先搜索)这颗树,每遍历一个节点,就要将其作为根节点从头到尾将整棵树全遍历一遍,但这样肯定就会超时了。
但其实每个节点的总距离和之间是有所关联的,但是比较难以察觉,这里借用灵茶山艾府的图片来解析。
先
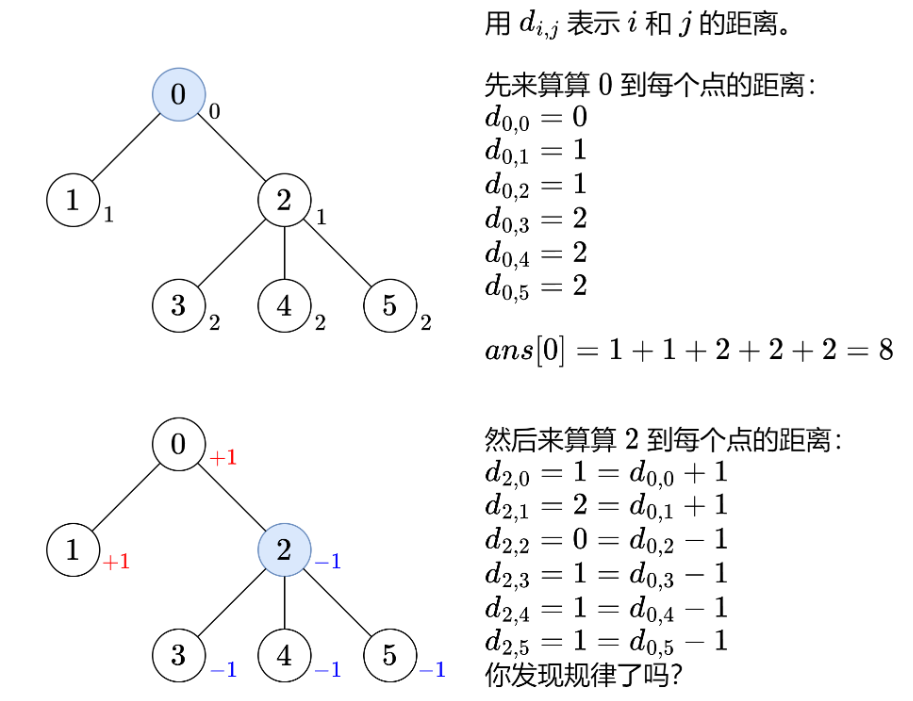
当遍历的节点从0换到2,我们可以发现结点2的子树距离都-1了,而非其子树的节点距离都+1了。所以我们只需要在节点0计算好的总距离之上做运算就能够得到其他结点的总距离了。我们可以看出只需要将父亲节点的总距离和加上除当前节点子树的节点数量再减去当前节点子树的节点数量即可得到当前节点的总距离和了。
我们可以得到递推公式:ans[2] = ans[0] + n – size[2] – size[2]
ans[2] = ans[0] + n – 2 * size[2]
当y节点为x节点的子节点时,y节点的距离总和就可以由x节点的距离总和通过递推公式推出:ans[y] = ans[x] + n – 2 * size[2]
但问题还没有解决,题目给出的并不是我们所熟悉的二叉树形式,而是将其所有的边以二维数组的形式给出。
所以一开始我们需要构图,将整个二叉树构建出来,但却并不需要真的创建出结构体来存储二叉树。还是使用二位数组来存放,主要的目的是方便我们dfs。
vector<vector<int>> g(n);
for (auto &e: edges) {
int x = e[0], y = e[1];
g[x].push_back(y);
g[y].push_back(x);
}将树上的每条边的两个节点用一个二维数组g存储,数组g的下标即代表了几号节点,其内容就是这个节点的邻居节点(所有相邻的节点包含父节点),以示例举例,edges = [[0,1],[0,2],[2,3],[2,4],[2,5]],那么构图之后得到的g数组:g = [[1,2],[0],[0,3,4,5],[2],[2],[2]]
代表的就是,g[0] = [1,2]节点0的邻居数组是节点1和节点2。
如此一来只要在递归的时候注意区分父节点就可以实现dfs了。
构建完二叉树后,我们需要算出每个节点的距离总和了,但就如前面的递推公式,我们需要节点0的距离总和才能递推出各个节点的距离总和。就像是普通动态规划题目一样的初始化,我们需要先初始化dp[0]这里也就是0节点的距离总和ans[0],所以我们需要先进行一次dfs来得到节点0的距离总和。
vector<int> ans(n); vector<int> size(n, 1); function<void(int, int, int)> dfs = [&](int x, int fa, int depth){ ans[0] += depth; for (int y: g[x]){ if (y != fa){ if (y != fa){ dfs(y, x, depth + 1); size[x] += size[y]; } } } };dfs(0, -1, 0);
计算距离总和的同时,我们也可以顺便记录一下递推公式中需要用到的值,各个节点其作为根节点的子树大小size[i].另外这里x,y之间的关系也比较绕,需要多看几遍多顺几遍可能才能搞清楚。定义一个整型数y在g[x]中遍历,后面放入的数会是0所以就是在g[0]中遍历节点0的邻居节点(因为节点0没有父节点所以fa为-1以使其不会触发for循环中的if语句),然后再进入下一层递归,递归g[1]中节点1的邻居节点,并且以0作为fa,如果y == fa会直接跳过,而size[1]一开始初始化就是1直接跳过那么得到的值也正是想要的1。void类型数组最后也不用写return会自动return。整体下来其实和普通的真正的二叉树深度遍历下来其实没有区别了。
接下来我们就可以带着ans[0]和size数组来算出所有节点的总距离和了。
function<void(int, int)> reroot = [&](int x, int fa){
for (int y: g[x]){
if (y != fa){
ans[y] = ans[x] + n - 2 * size[y];
reroot(y, x);
}
}
};
reroot(0, -1);
return ans;最后就比较好理解了,需要注意的同样也是y与x之间的父子关系,子节点y需要x父节点的总距离值才能推出答案。只需要将递归公式写上,再遍历下一层就好了
2368 受限条件下可到达节点的数目 题目描述:
现有一棵由 n 个节点组成的无向树,节点编号从 0 到 n - 1 ,共有 n - 1 条边。
给你一个二维整数数组 edges ,长度为 n - 1 ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。
在不访问受限节点的前提下,返回你可以从节点 0 到达的 最多 节点数目。
注意,节点 0 不 会标记为受限节点。
示例:
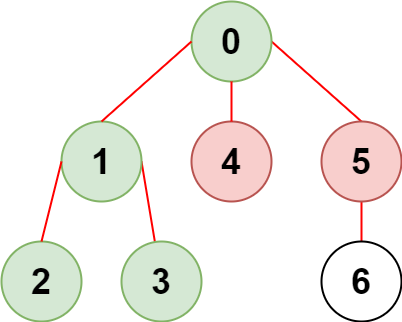
输入:n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5] 输出:4 解释:上图所示正是这棵树。 在不访问受限节点的前提下,只有节点 [0,1,2,3] 可以从节点 0 到达。
这题个人感觉就比较简单一些了,可能因为做过的上题比较相似,同样也是给出二叉树中的各条边,所以我们最先要做的就是构图
vector<vector<int>> g(n);
for (auto &e: edges){
int x = e[0], y = e[1];
g[x].push_back(y);
g[y].push_back(x);
}接着如果我们直接dfs遍历,然后遇到restricted数组中的节点的话就不继续往下遍历的话,就会卡在第61个超长测试用例,原因是在restricted数组中直接查找的时间太长了,每遍历一个节点就要遍历完整个restricted数组来查找这个节点是否在数组中,这样的操作无疑是十分重复的。所以我们可以将restricted数组转换成哈希表,这样查找时间就会变成O(1)了。
unordered_set<int> restrictedset;
for (int element : restricted) {
restrictedset.insert(element);
}这样一个个插入数组中还是比较繁琐,可以直接转换成哈希表
unordered_set<int> r(restricted.begin(), restricted.end());
function<void(int, int)> dfs = [&](int x, int fa){
ans += 1;
for (int y: g[x]){
if (y != fa && restrictedset.find(y) == restrictedset.end()){
dfs(y, x);
}
}
};
dfs(0, -1);
return ans;最后的dfs遍历就很简单了,查找当前遍历节点既不是父节点也不再restricted数组中的话就可以接着往下遍历了,并在途中增加总值就ok了。
2581 统计可能得树根数目 题目描述:
Alice 有一棵 n 个节点的树,节点编号为 0 到 n - 1 。树用一个长度为 n - 1 的二维整数数组 edges 表示,其中 edges[i] = [ai, bi] ,表示树中节点 ai 和 bi 之间有一条边。
Alice 想要 Bob 找到这棵树的根。她允许 Bob 对这棵树进行若干次 猜测 。每一次猜测,Bob 做如下事情:
-
- 选择两个 不相等 的整数
u和v,且树中必须存在边[u, v]。 - Bob 猜测树中
u是v的 父节点 。
- 选择两个 不相等 的整数
Bob 的猜测用二维整数数组 guesses 表示,其中 guesses[j] = [uj, vj] 表示 Bob 猜 uj 是 vj 的父节点。
Alice 非常懒,她不想逐个回答 Bob 的猜测,只告诉 Bob 这些猜测里面 至少 有 k 个猜测的结果为 true 。
给你二维整数数组 edges ,Bob 的所有猜测和整数 k ,请你返回可能成为树根的 节点数目 。如果没有这样的树,则返回 0。
示例:
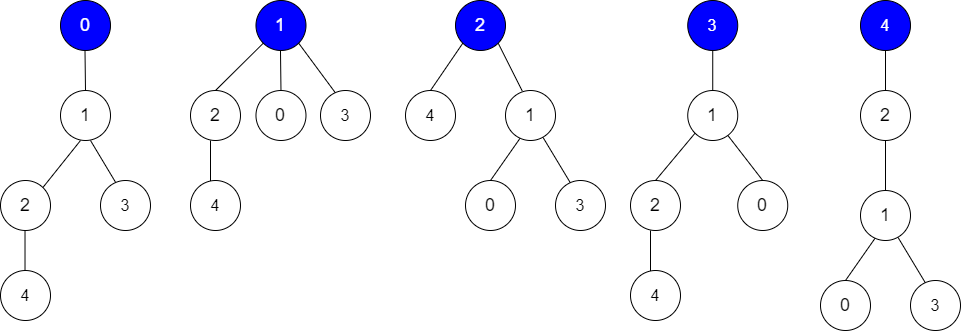
输入:edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3 输出:3 解释: 根为节点 0 ,正确的猜测为 [1,3], [0,1], [2,4] 根为节点 1 ,正确的猜测为 [1,3], [1,0], [2,4] 根为节点 2 ,正确的猜测为 [1,3], [1,0], [2,4] 根为节点 3 ,正确的猜测为 [1,0], [2,4] 根为节点 4 ,正确的猜测为 [1,3], [1,0] 节点 0 ,1 或 2 为根时,可以得到 3 个正确的猜测。
本题其实是我第一个遇到的这个类型的题目,所以做的非常艰难,题解也花了很长时间才理解,题解中推荐没接触过的人先去看上面的第一道题,所以我也把那道题放在前面了。这道题形式也相差不大,但想做好还是比较难的。首先的首先我们先把图构好。
vector<vector<int>> g(edges.size() + 1);
for (auto &e: edges){
int x = e[0], y = e[1];
g[x].push_back(y);
g[y].push_back(x);
}主要思路就是当我们换根的时候,比如从以0为根换到以1为根时,变化的边其实并不多,只有一条就是0与1之间的那条边,从以0为父节点变为以1为父节点,那其实我们就可以将以0节点为根节点时得到的正确的猜测数量减去以0为父节点以1为子节点的这个猜测的数量(当然有也最多只有一个),再加上以1为父节点以0为子节点的猜测,这样就可以得到以1节点为根节点时得到的正确的猜测数量了。就是因为其他地方都没有变化,只有0与1之间的父子关系颠倒了。
那么为了方便查找我们还是将猜测数组guesses转换为哈希表,不同的是,我们要将数组中两个数合并到一起方便我们查找,具体操作是将前面那个是左移32再或上后面那个数,因为这个整型数是32位的,所以这样操作两个数就不会有重叠的地方,产生的新的64位的数前面32位就还是两个数中前面那个,后面32位就是两个数中后面那个,这样就可以只用一个数来表示一条边了,同时还能区分父子关系,也就是[1,0]和[0,1]在这个哈希表中是不一样的。其中[1,0]在哈希表中表示的值为4294967296,[0,1]在哈希表中的值为1. 所以任何节点形成的边都可以在哈希表中以唯一的方式表示出来。
unordered_set<LL> s;
for (auto &e: guesses){
s.insert((LL) e[0] << 32 | e[1]);
}LL是long long类型的缩写
using LL = long long;但以后面节点为根的猜测数量需要以前面节点为根的猜测来递推。所以还是需要先将以0节点为根的猜测先用dfs遍历出来。
function<void(int, int)> dfs = [&](int x, int fa){
for (int y: g[x]){
if(y != fa){
cnt0 += s.count((LL) x << 32 | y);
dfs(y, x);
}
}
};
dfs(0, -1);这段也同样是理解好y与x之间的父子关系就能懂了。在哈希表s中查找是否有以x为父节点以y为子节点的边,因为存储在哈希表里的就是父节点在前子节点在后的形式的边。
接下来只需要再遍历以各个节点为根的树判断guesses数组中正确的边是否能达到k。
function<void(int, int, int)> reroot = [&](int x, int fa, int cnt){
ans += cnt >= k;
for (int y: g[x]){
if (y != fa){
reroot(y, x, cnt - s.count((LL) x << 32 | y) + s.count((LL) y << 32 | x));
}
}
};
reroot(0, -1, cnt0);
return ans;这里cnt - s.count((LL) x << 32 | y) + s.count((LL) y << 32 | x)其实就是前面我所说的将以x节点为根节点时得到的正确的猜测数量减去以x为父节点以y为子节点的这个猜测的数量,再加上以y为父节点以x为子节点的猜测。这句话就是本题的主要难点,这要理解了这个递推公式,这道题就迎刃而解了。
2369 检查数组中是否存在有效划分 题目描述:
给你一个下标从 0 开始的整数数组 nums ,你必须将数组划分为一个或多个 连续 子数组。
如果获得的这些子数组中每个都能满足下述条件 之一 ,则可以称其为数组的一种 有效 划分:
-
- 子数组 恰 由
2个相等元素组成,例如,子数组[2,2]。 - 子数组 恰 由
3个相等元素组成,例如,子数组[4,4,4]。 - 子数组 恰 由
3个连续递增元素组成,并且相邻元素之间的差值为1。例如,子数组[3,4,5],但是子数组[1,3,5]不符合要求。
- 子数组 恰 由
如果数组 至少 存在一种有效划分,返回 true ,否则,返回 false 。
示例:
输入:nums = [4,4,4,5,6] 输出:true 解释:数组可以划分成子数组 [4,4] 和 [4,5,6] 。 这是一种有效划分,所以返回 true 。
这题就比较轻松了,但同样也是动态规划的题目,需要前面得出的结果运用到后面的运算中。
主要就是三种情况,
1.如果最后两个元素相等,那么需要判断的就是开始到n – 2元素是否成有效划分
2. 如果最后三个元素相等,那么需要判断的就是开始到n – 3元素是否成有效划分
3. 如果最后三个元素成递增趋势,并差值都为1, 那么就是判断开始到n – 3元素是否成有效划分
把这三种情况的逻辑整理清楚那么这道题也就完成了。
接下来我们要定义dp数组的含义,dp[i + 1]表示从nums[0]到nums[i]的有效划分情况。
所以dp数组的大小我们需要设置成n + 1
vector<int> dp(n + 1);然后我们需要明确好递推公式,其实就是前面所说的三种情况
1.dp[i – 1] && (nums[i] == nums[i – 1])
2.dp[i – 2] && (nums[i] == nums[i – 1] && nums[i – 1] == nums[i – 2])
3.dp[i – 2] && (nums[i] == nums[i – 1] + 1 && nums[i] == nums[i – 2] + 2)
要注意第二第三种情况需要在i > 2的情况下才有结果。
接下来我们需要对dp数组进行初始化,因为我们前面定义了dp[i + 1]表示从nums[0]到nums[i]的有效划分情况,所以其实dp[0]其实是没有意义的,我们要直接将其初始化为true,这样就能方便后面的递推,但如果一开始dp数组的定义是dp[i ]表示从nums[0]到nums[i]的有效划分情况,那因为一个数一定不能成有效划分,就要将dp[0]初始化为false,就不太好操作了。
class Solution {
public:
bool validPartition(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n + 1);
dp[0] = true;
for (int i = 1; i < n; i++){
if (dp[i - 1] && nums[i] == nums[i - 1] ||
i > 1 && dp[i - 2] && (nums[i] == nums[i - 1] && nums[i] == nums[i - 2] ||
nums[i] == nums[i - 1] + 1 && nums[i] == nums[i - 2] + 2)){
dp[i + 1] = true;
}
}
return f[n];
}
};最后我们还需要注意if判断语句中的逻辑关系,这里是比较容易搞混的,第二第三种情况是可以用或的关系合并起来的,因为他们都有dp[i – 2]的部分。
这些就是这几天写的每日一题了,前两天没有更新博客,主要是想趁着好不容易撑过了两个月的训练营结束能好好休息一下,刚好又要坐高铁返校,就刚好休息了几天。明天开始我想要好好学学stm32了,争取这学期能学好,再做几个项目能写到简历里,最好再找到个好工作😋,可能一下子想太多了,先从明天开始做好吧,今天刚好买的stm32单片机也到了,明天就开始努力学吧!
今日分享歌曲:ワンダーランド——sakanaction(可惜这首歌要会员,感兴趣可以听听,非常好听捏,mvBV1hv411s7QR)
