今天带来三道题目：1261. 在受污染的二叉树中查找元素 ， 1254. 统计封闭岛屿的数目 ， 1129. 颜色交替的最短路径

1261. 在受污染的二叉树中查找元素 题目描述：

给出一个满足下述规则的二叉树：

1. 1. root.val == 0
   2. 如果 treeNode.val == x 且 treeNode.left != null，那么 treeNode.left.val == 2 * x + 1
   3. 如果 treeNode.val == x 且 treeNode.right != null，那么 treeNode.right.val == 2 * x + 2

现在这个二叉树受到「污染」，所有的 treeNode.val 都变成了 -1。

请你先还原二叉树，然后实现 FindElements 类：

• • FindElements(TreeNode* root) 用受污染的二叉树初始化对象，你需要先把它还原。
  • bool find(int target) 判断目标值 target 是否存在于还原后的二叉树中并返回结果

示例：

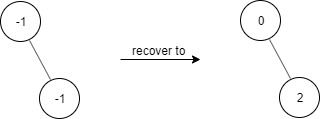
输入：
["FindElements","find","find"]
[[[-1,null,-1]],[1],[2]]
输出：
[null,false,true]
解释：
FindElements findElements = new FindElements([-1,null,-1]); 
findElements.find(1); // return False 
findElements.find(2); // return True

是好久没遇到的二叉树题目，很久没做二叉树递归了，正好拿这道题复习复习。

首先要做的就是将受污染的二叉树还原，很简单不复杂，根节点为0，其左子节点为父节点的二倍加一，右节点为父节点的二倍加二。

但是说还原但也不用真的还原，我们只是需要这些还原好的数用到接下来的判断中而已，只需要记录下来就好了。

void makeright(TreeNode* root, int val){
        if (root == NULL) return;
        numSet.insert(val);
        makeright(root -> left, val * 2 + 1);
        makeright(root -> right, val * 2 + 2);
    }

但我一开始有点不太熟悉写的有点复杂，真的把二叉树节点的值还原了，要说只是还原也不是很复杂，我把添加了判断当前节点是左孩子还是右孩子的操作，其实只要把孩子的值算出来再传递下去就好了。最后的判断也是比较简单了。

FindElements(TreeNode* root) {
        makeright(root, 0);
    }
    
    bool find(int target) {
        return numSet.contains(target);
    }

1254.统计封闭岛屿的数目 题目描述：

二维矩阵 grid 由 0 （土地）和 1 （水）组成。岛是由最大的4个方向连通的 0 组成的群，封闭岛是一个 完全 由1包围（左、上、右、下）的岛。

请返回 封闭岛屿 的数目。

示例：

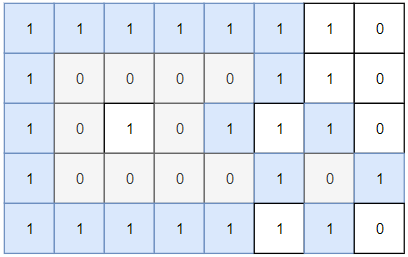
输入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
输出：2
解释：
灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。

首先我们要明确封底岛屿是怎么样的定义，就是不与边界领域接触的岛屿，题目解释的不是很清晰，我还是看题解的时候才搞清楚的。明确这点后其实就比较清晰了，这题和前两天做的130.被围绕的区域很像，做法也差不多，就是现在四周边界区域搜索陆地，先把与边界相连的陆地都标记为水域，这样剩下的陆地肯定就是不与边界领域接触的岛屿了，也就是我们所要求的岛屿数量了。

int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    
    void dfs(vector<vector<int>>& grid, int x, int y){
        grid[x][y] = 1;
        for (int i = 0; i < 4; i++){
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            if (nextx >= 0 && nextx < grid.size() && nexty >= 0 && nexty < grid[0].size() && grid[nextx][nexty] == 0){//边界条件，如果下个点是岛屿就可以遍历
                dfs(grid, nextx, nexty);
            }
        }
    }

首先是dfs深度优先搜索的函数先把它定义好，这是遍历岛屿并将其标记为水域的dfs函数。

int closedIsland(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        

        for (int i = 0; i < n; i++){
            if (grid[i][0] == 0) dfs(grid, i, 0);//先遍历左边界一列
            if (grid[i][m - 1] == 0) dfs(grid, i, m - 1);//遍历右边界一列
        }
        for (int j = 0; j < m; j++){
            if (grid[0][j] == 0) dfs(grid, 0, j);//遍历上边界一行
            if (grid[n - 1][j] == 0) dfs(grid, n - 1, j);//遍历下边界一行，并将其搜索到与边界接触的陆地都标记成海域
        }
        
        int ans = 0;

        for (int i = 1; i < n - 1; i++){
            for (int j = 1; j < m - 1; j++){
                if (grid[i][j] == 0){
                    ans++;遇到陆地就可以++，因为后面dfs函数会把这块岛屿都标记成水域，下次再遇到陆地就是另一个岛屿了。
                    dfs(grid, i, j);
                }
            }
        }
        
        return ans;
    }

1129. 颜色交替的最短路径 题目描述：

给定一个整数 n，即有向图中的节点数，其中节点标记为 0 到 n - 1。图中的每条边为红色或者蓝色，并且可能存在自环或平行边。

给定两个数组 redEdges 和 blueEdges，其中：

• • redEdges[i] = [ai, bi] 表示图中存在一条从节点 ai 到节点 bi 的红色有向边，
  • blueEdges[j] = [uj, vj] 表示图中存在一条从节点 uj 到节点 vj 的蓝色有向边。

返回长度为 n 的数组 answer，其中 answer[X] 是从节点 0 到节点 X 的红色边和蓝色边交替出现的最短路径的长度。如果不存在这样的路径，那么 answer[x] = -1。

示例：

输入：n = 3, red_edges = [[0,1],[1,2]], blue_edges = []
输出：[0,1,-1]

本题给的描述和示例我感觉都有点模糊，其实就是每个节点到始发节点0的最短路径，可以是只有红色路径的，也可以是只有蓝色路径的，也可以是红蓝都有的。像是最短路径我们一般都会选择使用广度优先搜索，因为广度优先搜索第一次遍历到的节点就是到这个节点的最短路径。

首先我们需要把红色路径和蓝色路径的始终节点都先记录下来，这里我们使用一个三维数组来记录。用于后面的搜索中。

vector<vector<vector<int>>> g(2, vector<vector<int>>(n));
        for (auto & e : redEdges){
            g[0][e[0]].push_back(e[1]);//g[0]表示的都是红色的路径
        }
        for (auto & e : blueEdges){
            g[1][e[0]].push_back(e[1]);//g[1]表示的都是蓝色的路径
        }

接下来是广度搜索要用到的队列，有两个参数，一个是当前节点，第二个表示的是当前边的颜色（红色为0， 蓝色为1）

queue<pair<int, int>> q;
        q.push(make_pair(0, 0));
        q.push(make_pair(0, 1));

vector<vector<bool>> vis(n, vector<bool>(2, false));//访问数组，用于判断当前节点是否已经访问过
        vector<int> ans(n, -1);//结果数组
        int d = 0;//当前节点到始发节点的距离

接下来就是广度搜索的过程了，我们一开始在队列里放了节点0的路径情况，程序就会将节点0的邻居节点，也就是能够直接去到的节点的路径都放入队列里，以用于下一层的遍历。

while (!q.empty()){
            for (int k = q.size(); k; --k){
                auto [i, c] = q.front();//先是遍历颜色c路径
                q.pop();
                if (ans[i] == -1){
                    ans[i] = d;
                }
                vis[i][c] = true;
                c ^= 1;//异或操作转换颜色，比如红色转换成蓝色，但队列里还有一个蓝色的路径，等到下一次循环的时候蓝色又会变成红色了
                for (int& j : g[c][i]){//这样的程序写法就能够比较统一
                    if (!vis[j][c]){
                        q.push(make_pair(j, c));//将邻居节点放入队列中用于下一层遍历。
                    }
                }
            }
            ++d;//到下一层遍历了，距离++，注意所谓的距离就是路径，两个由路径相连的节点距离差为1.
        }

需要注意的是，我们每一次都会把红色路径和蓝色路径都分别遍历一次，并且每次分别的遍历都会转换成另外一个颜色。

这两天没怎么学stm32的东西，因为最近看到代码随想录推荐的一个人工智能的培训机构，看的我有点心动，还在考虑要不要放弃单片机嵌入式去学人工智能，但今天问了一下老师之后觉得还是学好本专业的东西比较好，毕竟这个专业就业还是挺多的，而且也学了这么久学过来了，又去学别的东西有点没必要，费时又费力，还不如去参加一些物联网嵌入式的培训班。现在确定要学这个了就赶紧静下心来好好学吧。

今日推荐歌曲シャンディガフ——sakanaction（点击左下角倒数第7首即可收听）