今天带来三道题目：

238. 除自身以外数组的乘积 ， 41. 缺失的第一个正数 ， 234. 回文链表

238.除自身以外数组的乘积 题目描述：

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在  32 位 整数范围内。

请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

示例：

输入: nums = [1,2,3,4] 输出: [24,12,8,6]

输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

本题明确要求了不能够使用除法来解决，不然的话就太简单了，直接算出所有数的乘积再逐个除以每个元素就行了。但不能使用除法也没关系，我们总有办法的，说到底要求的就是除了自身之外的所有数的乘积，我们先把答案数组和原数组列出来。

A数组代表原数组，b数组代表答案数组。

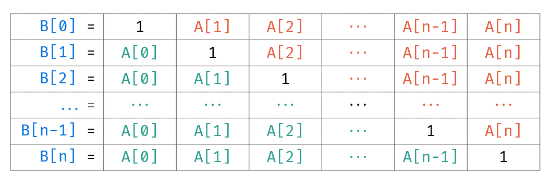
由图我们可以看出，其实只要将当前元素看作是1再与其他数相乘就行，我们还可以再把其他要乘的数分成左右两边，为了整体统一我们最好能够先算出左半边的乘积再乘以右半边的乘积，这样就会方便很多，只需要遍历两次，计算左半边乘积一次，计算右半边乘积一次。

先定义一些变量：

int len = nums.size();
        if (len == 0) return {};
        vector<int> result(len, 1);
        result[0] = 1;//初始化
        int temp = 1;//存储右半边乘积

接下来遍历计算左半边的乘积：

for (int i = 1; i < len; i++){
            result[i] = result[i - 1] * nums[i - 1];//因为只有左半边的乘积，所以下一个元素的答案肯定是这个元素的答案再乘以当前这个元素
        }

最后遍历计算右半边的乘积：

for (int i = len - 2; i >= 0; i--){//因为最后一个元素已经在上一个遍历中把左边全部需要的乘积都算好了，所以就可以不用管最后一个了
            temp *= nums[i + 1];//存储右半边的乘积，和前一个遍历计算的操作相同，下一个元素的右半边乘积肯定是当前元素的右半边元素乘积乘以当前元素
            result[i] *= temp;//将temp里存储的右半边乘积乘以答案数组里的左半边乘积就能得到答案了。
        }

41.缺失的第一个正数 题目描述：

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

示例：

输入：nums = [1,2,0]
输出：3
解释：范围 [1,2] 中的数字都在数组中。

输入：nums = [3,4,-1,1]
输出：2
解释：1 在数组中，但 2 没有。

输入：nums = [7,8,9,11,12]
输出：1
解释：最小的正数 1 没有出现。

本题要求只能够使用常熟级别额外空间，所以不能再使用哈希表来进行查找，但其实原数组本身就可以是一个哈希表，毕竟哈希表本来就有以数组的形式存在的，首先我们要明确，这个原数组如果全都是正整数并且有着从1到nums.size()所有连续的整数的话，说明我们要找的最小的正整数是nums.size() + 1,如果不是的话我们要找的肯定就是1到nums.size()之间的一个数。

主要的方法就是把各个数放到对应的下标，如果有不对应的下标，说明我们就找到了最小的正整数了。

我们把1对应到下标0,2对应到下标1，数i对应到下标i – 1，我们可以先遍历一遍使用交换函数把正整数元素都放到对应的下标上，完事后我们再遍历一遍看有没有对应不到元素的下标，如果有的话就说明这个下标i对应的数i + 1就是我们要找的那个正整数。如果没有的话说明整个数组都是正整数并且从1到nums.size()的数都有。

首先遍历将数都排序放好：

for (int i = 0; i < nums.size(); i++){
            while (nums[i] != i + 1){
                if (nums[i] <= 0 || nums[i] > nums.size() || nums[i] == nums[nums[i] - 1]) break;//如果数不是正整数并且不在nums.size()范围我们就可以跳过
                int idx = nums[i] - 1;//交换操作
                nums[i] = nums[idx];
                nums[idx] = idx + 1;
            }
        }

需要注意的是我们这里判断的条件是nums[i] == nums[nums[i] - 1]而不是i == nums[i] – 1，因为i == nums[i] – 1可能会导致死循环，在交换元素后，如果新的nums[i] 恰好等于 i+1，就会陷入死循环。

最后再检查中间是否有缺少的数即可：

for (int i = 0; i < nums.size(); i++){
            if (nums[i] != (i + 1)){
                return (i + 1);
            }
        }
        return nums.size() + 1;

234.回文链表 题目描述：

给你一个单链表的头节点 head ，请你判断该链表是否为

。如果是，返回 true ；否则，返回 false 。

示例：

输入：head = [1,2,2,1]
输出：true

本题普通的解法其实不难，就是遍历一遍然后将值存入数组中，再判断这个数组是否形成回文：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    bool isPalindrome(ListNode* head) {
        vector<int> judge;
        ListNode* cur = head;
        while (cur){
            judge.push_back(cur -> val);
            cur = cur -> next;
        }
        if (judge.size() == 1) return true;
        for (int i = 0, j = judge.size() - 1; i <= j; i++, j--){
            if (judge[i] != judge[j]) return false;
        }
        return true;
    }
};

但是有一个递归的方法很有意思，这里再分享一下

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
    ListNode* frontPointer;
public:
    bool recursivelyCheck(ListNode* currentNode) {
        if (currentNode != nullptr) {
            if (!recursivelyCheck(currentNode->next)) {//如果后面的节点传回来的false说明后面已经有对不上的节点了。遍历到最后节点会跳过这里直接return true，所以从倒数第一个节点会开始比较
                return false;
            }
            if (currentNode->val != frontPointer->val) {//递归遍历到后面会从最后一个节点开始与第一个节点比较比较。
                return false;
            }
            frontPointer = frontPointer->next;//比较结果相等的话前面的frontpointer就往后走
        }
        return true;
    }

    bool isPalindrome(ListNode* head) {
        frontPointer = head;
        return recursivelyCheck(head);
    }
};