今天带来的题目是1976. 到达目的地的方案数 , 49. 字母异位词分组
1976.到达目的地的方案数 题目描述:
你在一个城市里,城市由 n 个路口组成,路口编号为 0 到 n - 1 ,某些路口之间有 双向 道路。输入保证你可以从任意路口出发到达其他任意路口,且任意两个路口之间最多有一条路。
给你一个整数 n 和二维整数数组 roads ,其中 roads[i] = [ui, vi, timei] 表示在路口 ui 和 vi 之间有一条需要花费 timei 时间才能通过的道路。你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。
请返回花费 最少时间 到达目的地的 路径数目 。由于答案可能很大,将结果对 109 + 7 取余 后返回。
示例:
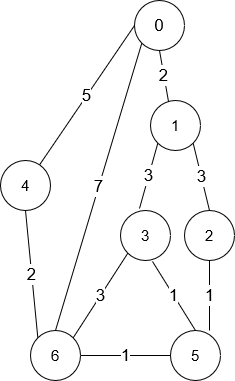
输入:n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]] 输出:4 解释:从路口 0 出发到路口 6 花费的最少时间是 7 分钟。 四条花费 7 分钟的路径分别为: - 0 ➝ 6 - 0 ➝ 4 ➝ 6 - 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6 - 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
本题主要需要运用到Djkstra算法的知识,这个算法主要是为了求始发节点到终点节点的最短路径
需要记录到达每个节点的最短路径的长度,以及到达每个节点的最短路径的上一个节点名,这样就不用记录整个长串的路径名了,因为始发节点只会有一个,只记录上一节点的名字即可寻回最短路径。
具体的实现方法是,先遍历始发节点和与其相连的节点的连接情况。然后更新路径长度数组中到达相连节点的最短距离。并分别记录这些节点的上一节点为始发节点。再遍历这些与始发节点相邻的节点与其他结点的连接情况,与其相连的节点的距离如果再路径长度数组中有记载到该节点的最短距离,那么就可以比较本节点到这个节点的距离加上本节点到始发节点的距离是否比这个记录的最短距离要更短。
基本上Djkstra算法就是这样记录更新始发节点到各个节点的最短路径的。但没有图片配合讲解基本上很难理解清楚的,这里主要还是抛砖引玉,这个算法也挺有意思的,但b站比较细致的讲解不太多,等以后有机会再碰到Djkstra的算法,再细致的讲解一下,这里其实用到的方法和正统的Djkstra算法还不太一样。
这里需要定义一个g[i][j],表示节点i到节点j之间需要花费的时间,如果没有直接到达的路径,则是初始化好的正无穷即LLONG_MAX。
还要一个dis[i]记录始发节点到达i节点的最短距离。初始化d[0]为0,其他的都初始化为正无穷,以便后面对比最短路径所用。
最后还需要一个f[i]来记录始发节点到达i节点最小时间花费的路径数。
首先我们先记录下相连节点之间来往所需要花费的时间:
vector<vector<long long>> g(n, vector<long long>(n, LLONG_MAX / 2));//这样初始是为了后续操作不溢出
for (auto &r : roads){
int x = r[0], y = r[1], d = r[2];
g[x][y] = d;
g[y][x] = d;
}接下来我们来初始化dis数组和f数组:
vector<long long> dis(n, LLONG_MAX / 2);
dis[0] = 0;
vector<int> f(n), done(n);
f[0] = 1;接下来就是我们这道题的主要逻辑,也是解决这道题的关键之处,在dis数组中,我们找到最小的那个元素,比如是5,那么我们从始发节点到达节点5的花费时间是我们到达所有节点中花费时间最短的,那么我们从始发节点到达节点5的最小路径也是可以确定的,不可能从始发节点到其他结点再到节点5的花费时间能够比从始发节点直接到节点5要短了。而且从始发节点到节点5再到其他结点就是最有机会更新其他节点最短路径的方案了,所以我们可以对比
dis[5](从始发节点到节点5) + g[5][y](节点5到其他结点y) 与 dis[y](直接从始发节点到节点y)
这样我们的思路就很明确了,如果dis[5] + g[5][y] > dis[y]的话,那么其实到达节点y最短路径的数量(注意是数量)等于到达节点5的最短路径的数量是一样的,因为只是到达节点5的最短路径再加上从节点5到节点y的这一条路径就到达节点y而已,并没有更多的其他路径,只是道路的延长而已,最短路径的数量是没有变的。
如果dis[5] + g[5][y] == dis[y]的话,那么说明dis[5] + g[5][y]是一条新的最短路径,只需要将f[y] += f[5]即可。
while(true){
int x = -1;
for (int i = 0; i < n; i++){
if (!done[i] && (x < 0 ||dis[i] < dis[x])){
x = i;
}
}
if (x == n - 1){
return f[n - 1];//最终返回放在这里而不是函数最后
}
done[x] = true;//done数组表示始发节点到该节点路径最短,以将其屏蔽,不会影响到下一循环寻找次短的路径
for (int y = 0; y < n; y++){
long long new_dis = dis[x] + g[x][y];
if (new_dis < dis[y]){
dis[y] = new_dis;
f[y] = f[x];
}
else if (new_dis == dis[y]){
f[y] = (f[y] + f[x]) % 1000000007;
}
}
}49.字母异位词分组 题目描述:
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
示例:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"] 输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
本题是哈希表比较经典的应用题目,我们其实不需要去判断单词和单词之间各个字母是不是相等之类的。首先我们需要建立一个键值对类型的哈希表,以单词排好序后的字符串作为键,以存放单词字符串的数组作为值,这样我们就可以遍历每个单词字符串,每遍历一次就找到当前单词排序好的字符串的键,并把当前单词存入到作为值的数组中。最后再将这些数组一一输入到一个二维数组中即可。
unordered_map<string, vector<string>> mp;//使用map类型,可使用键值对类型,而set类型不可。
for (auto t : strs){
string key = t;
sort(key.begin(), key.end());
mp[key].push_back(t);
}vector<vector<string>> res;
for (auto t : mp){
res.push_back(t.second);
}
return res;这两天其实也刷了挺多题,但主要还是练习的多,值得单另出来讲的不是很多,明天估计就会多一些了,因为明天周五安排的题量会多一点,希望能尽量都消化好吧,今天晚上还学了一下stm32的内容,主要收获是理解了寄存器编程和函数编程的主要区别,寄存器编程呢,比较麻烦一些,需要去查操作手册,了解哪个寄存器的哪几位操作什么然后再进行修改,而且还要防止修改其他位导致之前做好的配置被修改,要用&=,|=的操作来修改。
函数编程其实也挺麻烦,可能熟悉了就好一些,首先你得清楚那个函数可以帮你操作,比如函数RCC_APB2PeriphClockCmd,是APB2内设时钟控制,能操作内设时钟使能和失能,但具体使用的参数还要查函数定义,不过这个就比较方便一点了,直接在keil右键这个函数就能去到头函数文件中查看,比查操作手册什么的就确实是方便许多了。不过操作的东西就比较多了,像是GPIO_Init函数就需要再创建一个结构体来供函数参数使用,结构体的创建又需要在头函数文件中搜索查找,但整体都还是有迹可循,可以一步一步地去找到操作指南,直接看操作手册的话确实会难找很多。今天最终能够实现pc13指示灯的点亮与熄灭。


