今天带来四道题目:15. 三数之和 , 11. 盛最多水的容器 , 200. 岛屿数量 , 695. 岛屿的最大面积
15. 三数之和 题目描述
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]] 解释: nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意,输出的顺序和三元组的顺序并不重要。
本题可用双指针的方法来解决,令人疑惑的一点是,我们要求三个数的和,只用双指针两个指针怎么够呢,没错,就是不够,那也不是什么大问题,不够再加一个不就行了,遍历一个数时,设这个数的下一位为left,数组中最后一位为right。这样就能从两边往中间遍历双指针来找出能让当前遍历元素组成和为0的另外两个数了。
当然直接这样设定left和right指针是很难有思路的,我们需要在一开始先将整个数组进行排序,这样负数就会在前面,正数就会在后面。当我们的当前遍历元素遍历到正数时其实就说明我们需要找的三数之和的组合已经找齐了,因为当前遍历元素为正数时left和right指针所指的元素应该也为正数,不可能再找到和为0的三个数了。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> result;
sort(nums.begin(), nums.end());
for (int i = 0; i < nums.size(); i++){
if (i > 0 && nums[i] == nums[i - 1]) continue;
int left = i + 1;
int right = nums.size() - 1;
while (left < right){
if (nums[i] + nums[left] + nums[right] < 0) left++;//总和小于0说明负数的部分太小,需要增大
else if (nums[i] + nums[left] + nums[right] > 0) right--;//总和大于0说明正数的部分太大,需要减小
else {
result.push_back({nums[i], nums[left], nums[right]});
while (left < right && nums[right] == nums[right - 1]) right--;//遇到相同的就跳过
while (left < right && nums[left] == nums[left + 1]) left++;
left++;
right--;
}
}
}
return result;
}
};11.盛水最多的容器 题目描述:
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例:

输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
本题同样也是双指针的经典应用题目,首先我们需要明确的是容器的两边是取小的那个边来算能够容纳水的最大值,所以我们可以转变思路,不是从最大的边下手,而是先从小的那边下手,设定left指针指向索引0,right指针指向最后,对比两个指针指向的元素,记录下两条边能够容纳的水,再让小的那边的指针往中间移,循环往复我们就能够得到能够容纳水的最大值了。
class Solution {
public:
int maxArea(vector<int>& height) {
int front = 0;
int back = height.size() - 1;
int square = 0;
int result = 0;
while (front < back){
square = (back - front) * min(height[front], height[back]);
result = square > result ? square : result;
if (height[front] > height[back]) back--;
else front++;
}
return result;
}
};200,岛屿数量 题目描述:
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例:
输入:grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] 输出:1
后面这两道图论题就上强度了,因为第一次接触还不是很熟悉,不是那么好消化,先理解好一个解法,其他的下次比较熟悉之后再来了解。
这里带来的是深度优先遍历方法dfs,这种二维网格遍历的题目,我们需要先设定一个方向数组,方便后面往上下左右的遍历。
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};这里就是制作了一个上下左右的偏移量。dir[x][0],dir[x][1]就分别代表了x,y的偏移量。
- 右:(0, 1)
- 下:(1, 0)
- 左:(0, -1)
- 上:(-1, 0)
dfs递归遍历的算法主要就是分别往这四个方向去遍历grid数组。dfs与bfs不一样的就是dfs会一直往一个方向去遍历,直到遇到不符合条件的点,bfs会一直遍历上一节点的周围节点,一圈一圈的往外遍历。这里给出的是dfs的遍历方式。
void dfs (vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y){
for (int i = 0; i < 4; i++){
int nextx = x + dir[i][0];//添加下个节点的x轴方向的偏移量
int nexty = y + dir[i][1];//添加下个节点的y轴方向的偏移量
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;//防止过界,直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1'){
visited[nextx][nexty] = true;
dfs(grid, visited, nextx, nexty);
}
}
}这种dfs遍历方法没有设定终止条件,因为最后的if判断语句就是判断下一节点是否符合要求,不符合的就直接不去递归遍历了,这样就节省了一些操作。下面是正常操作有终止条件判断的代码,建议还是使用前面的代码。
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
if (visited[x][y] || grid[x][y] == '0') return;
visited[x][y] = true; // 标记访问过
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
dfs(grid, visited, nextx, nexty);
}
}这段函数遍历一次后,就会把同一个岛屿的陆地的访问数组都标记为已访问,就可以实现统计岛屿数量的要求了。
int numIslands(vector<vector<char>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
if (!visited[i][j] && grid[i][j] == '1'){
visited[i][j] = true;
result++;
dfs(grid, visited, i, j);
}
}
}
return result;
}还是需要遍历每个点,来查询其访问节点,如果为访问过,那么dfs函数就会将这个岛屿所拥有的所有陆地全都标记为已访问,那么下次再遍历到同岛屿的陆地时,就可以直接跳过了。
695.岛屿的最大面积 题目描述:
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例;
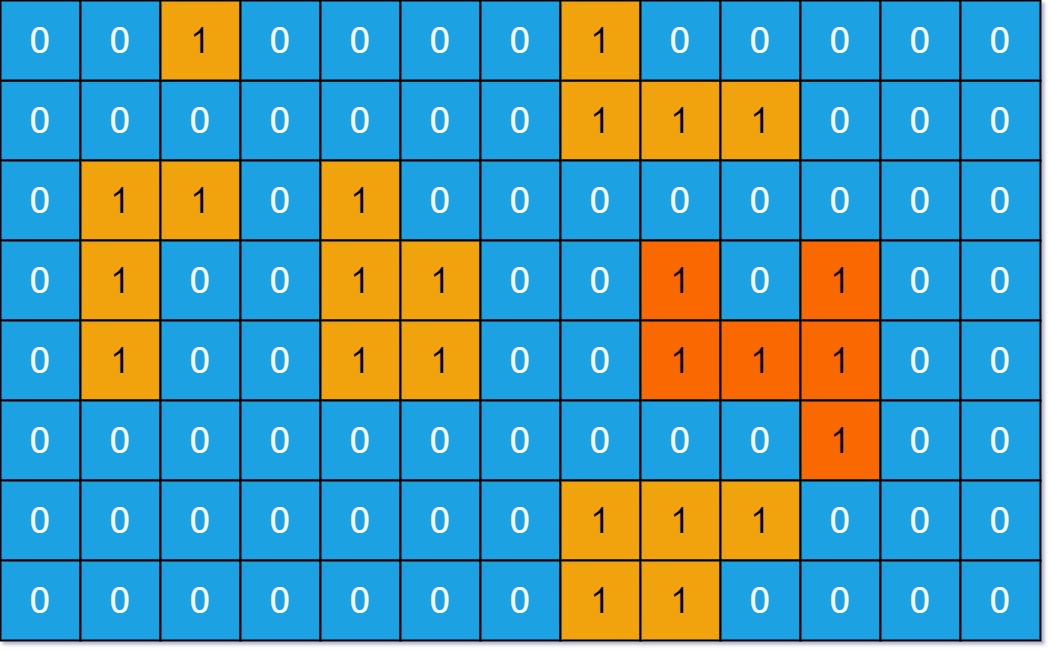
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,1,1,0,1,0,0,0,0,0,0,0,0], [0,1,0,0,1,1,0,0,1,0,1,0,0], [0,1,0,0,1,1,0,0,1,1,1,0,0], [0,0,0,0,0,0,0,0,0,0,1,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出:6 解释:答案不应该是11,因为岛屿只能包含水平或垂直这四个方向上的1。
本题和上一题其实比较相似,递归遍历函数基本不用改很多,只是把统计访问数组改成了统计岛屿面积大小。
int count;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y){
for (int i = 0; i < 4; i++){
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1){
visited[nextx][nexty] = true;
count++;
dfs(grid, visited, nextx, nexty);
}
}
}只需要再最后判断下一个节点是否符合条件是的执行操作中加入count++即可。
但这种解决办法还少了第一次进入递归遍历时的那块陆地的面积1,因为这个遍历的操作只会将下一符合条件的陆地节点的面积加入到count中,不会将本节点的面积加入,因为在上一层递归中已经加过了,但在第一次递归的时候的面积还是没有加的,所以我们需要将count初始化成1。
int maxAreaOfIsland(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
if (!visited[i][j] && grid[i][j] == 1){
count = 1;
visited[i][j] = true;
dfs(grid, visited, i, j);
result = result > count ? result : count;
}
}
}
return result;
}完整代码
class Solution {
private:
int count;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y){
for (int i = 0; i < 4; i++){
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1){
visited[nextx][nexty] = true;
count++;
dfs(grid, visited, nextx, nexty);
}
}
}
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
if (!visited[i][j] && grid[i][j] == 1){
count = 1;
visited[i][j] = true;
dfs(grid, visited, i, j);
result = result > count ? result : count;
}
}
}
return result;
}
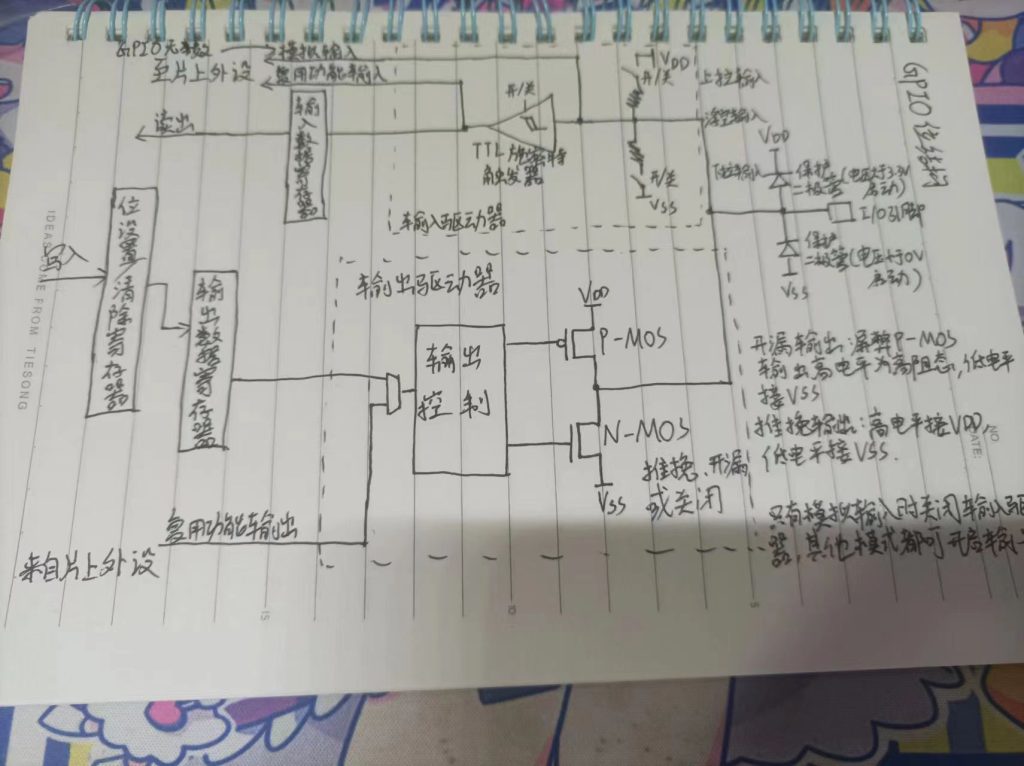
};今天stm32的学习主要学了GPIO位结构,主要是输出输入的各种模式,及其原理。主要还是要记的东西会比较多。把图画了画,有时间还是要多记多看多熟悉。
今日推荐歌曲ショック!——sakanaction(点击左下角,倒数第六首即可收听)
