今天带来的题目是:
34. 在排序数组中查找元素的第一个和最后一个位置 , 2386. 找出数组的第 K 大和 , 239. 滑动窗口最大值 ,1020. 飞地的数量 , 417. 太平洋大西洋水流问题
34.再排序数组中查找元素的第一个和最后一个位置 题目描述:
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例:
输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4]
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1]
本题主要考察的是二分查找的用法,二分查找最关键的点就是在于分清楚遍历区间的左右指针是左闭右闭,还是左闭右开,还是左开右开。
以下是三种情况各自左右指针的定义即判断条件:
左闭右闭:left = 0, right = nums.size() – 1 ,(left <= right)
左闭右开:left = 0, right = nums.size(),(left < right)
左开右开:left = -1, right = nums.size(),(left + 1 < right)
还有就是二分查找最后找到的元素的下标:
左闭右闭: 左指针会指向目标值,但右指针会指向目标值的前一位,因为左右指针同时指向目标值时判断条件会判断成中值等于目标值在中值大于等于目标值的判断范围内,所以right = mid – 1,最后目标值的下标是left
左闭右开:因为最后right应该指向目标值的前一位,但是这里right是开区间,所以会后移一位,最终left和right都会指向目标值。
左开右开:在左闭右开基础上左边又变成了开区间,向前移一位,最后right指向目标值
这些对照着代码,代入运算一下就会好理解一些了。
int loudfind(vector<int>& nums, int target){
int left = 0;
int right = nums.size() - 1;
while (left <= right){
int mid = left + (right - left) / 2;
if (nums[mid] < target) left = mid + 1;
else right = mid - 1;
}
return left;
}本题是可以使用寻找大于等于target的值的模型来做,第一个出现的target就可以用大于等于来查找,最后一个出现的就可以用小于target+1的值来进行查找了,找到这个值的下标之后再-1,就能得到最后出现的target在哪了。
vector<int> searchRange(vector<int>& nums, int target){
int start = loudfind(nums, target);
if (start == nums.size() || nums[start] != target){
return vector<int>({-1, -1});
}
int end = loudfind(nums, target + 1) - 1;
return vector<int>({start, end});
}2386.找出数组的第k大和 题目描述:
给你一个整数数组 nums 和一个 正 整数 k 。你可以选择数组的任一 子序列 并且对其全部元素求和。
数组的 第 k 大和 定义为:可以获得的第 k 个 最大 子序列和(子序列和允许出现重复)
返回数组的 第 k 大和 。
子序列是一个可以由其他数组删除某些或不删除元素排生而来的数组,且派生过程不改变剩余元素的顺序。
注意:空子序列的和视作 0 。
示例:
输入:nums = [2,4,-2], k = 5 输出:2 解释:所有可能获得的子序列和列出如下,按递减顺序排列: - 6、4、4、2、2、0、0、-2 数组的第 5 大和是 2 。
本题是今天的每日一题,但是还是非常难的,题解看了大半天也不是很清楚,本来应该有挺多种解法,这里就先学好二分查找加暴力搜索的解法,其他的以后再说吧。
首先我们先想一想这个数组我们能够的道德最大的子序列和是什么样的,是不是应该是所有的正数相加之和。这是一个需要先明确的点,然后我们可以在这个最大的和上面进行操作得到次大的和,可以是去除正数的元素,比如例子中正数相加是2 + 4 = 6,我们去除掉元素2,就能得到序列和4了,我们也可以通过加上负数,比如6 + (-2) = 4,也能够得到序列和4。所以其实我们只需要在最大序列和之上做减法就可以了。那为了方便我们做减法,我们可以把这个数组里的负元素全都转变为绝对值,这样我们就可以在最大序列和上做绝对值数组的减法了,这样就能找到所有的子序列和了。
long sum = 0;
for (int &x : nums){
if (x >= 0){
sum += x;
}
else {
x = -x;
}
}
ranges :: sort(nums);再将已经绝对值化的数组排好序这样就能够得到从小到大排好的数组,我们将最大序列和sum减去最小的元素就能得到次大的子序列和了。能够方便后面寻找第k大和。
接下来我们需要使用二分查找和深度优先搜索的方法来找到第k大子序列和,这里是比较难以理解的,我消化了大半天还是感觉有点懵。但大体的思路还是清晰的。
auto check = [&](long sum_limit) -> bool {
int cnt = 1;
function<void(int, long long)> dfs = [&](int i, long long s){
if (cnt == k || i == nums.size() || s + nums[i] > sum_limit){//如果大于当前二分查找给出的边界sum_limit,说明最小的k个元素之和在sum_limit之上
return;
}
cnt++;//当前和没有超过sum_limit,可以在继续往深处遍历
dfs(i + 1, s + nums[i]);//选择当前遍历到的元素nums[i]
dfs(i + 1, s);//不选择当前遍历的元素nums[i]
};
dfs(0, 0);
return cnt == k;
};这是查找可以被最大序列和sum减去的k个元素的和,sum减去这个和之后就能够得到第k大序列和了,而这个k个元素的和需要我们使用二分查找法来找到,查找的范围呢,就是0到nums数组的总和(已绝对值化)。
long long left = -1, right = accumulate(nums.begin(), nums.end(), 0LL);
while (left + 1 < right){
long long mid = left + (right - left) / 2;
(check(mid) ? right : left) = mid;//如果中间值mid为true说明,最小的k个元素和比值mid要小,将right值赋值为mid,以查找left与原mid值之间的最小的k个元素之和
}
return sum - right;因为我们是在0到nums数组所有元素之和这段值里面查找的k个元素的最小和,而且这是前面说到的左开右开的形式,最后找到的值就是right,最大序列和sum减去right就能够得到第k大的序列和。
239.滑动窗口最大值 题目描述:
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
本题之前在代码随想录训练营中做过,所以还是比较熟悉的,但具体解法还是忘得差不多了,毕竟也是差不多两个月之前做的了。现在正好可以来回顾一下。本题可以使用单调队列来做,之前第一次接触到这题的时候,没有学单调栈,对这种数据结构的使用还很陌生,当时就记得看视频讲解不明不白的,最后也是把答案抄上去就完事了,现在学过单调栈再来看这个用单调队列做的题目就感觉亲切很多了。
本题的主要思路就是像单调栈那样,自始至终让队列里的数,从队首到队尾成一个单调递减的趋势,这样我们要求的最大值就可以一直保留在队首了,获取起来也很方便。实现这个单调队列的主要有三个函数,pop函数、push函数、getvalue函数。
最重要的思想就是,要让最大值一直都保留在队首,这样就只需要维护最大值就可以了,举例来说,一开始滑动窗口要放入1, 3, -1三个元素,但我们在放入队列时,操作就不太一样了,首先是元素1入队,这是它是最大的,也在队首待着,但当元素3加入时,这时元素3是最大的,但它的前面的元素1比它小,为了保证最大元素永远在队首,我们就可以直接把元素从队首弹出,这样元素3就可以在队首待着了,再到元素-1加入时,它前面的元素3不比-1小,队首到队尾成单调递减趋势,所以可以不用将元素3弹出。
再到下一个元素-3加入滑动窗口,元素1退出滑动窗口时,元素1就不用再在队列中弹出了,因为元素3加入的时候已经把它给卷走了。-3因为小于-1也可以直接地加入到队列当中。再到元素5加入到滑动窗口,元素3退出滑动窗口,这时要将队列的最大值弹出队列,就需要操作pop函数将其弹出了,再加入元素5时,因为它比前面的-1,-3都要大,为了保持队列的单调递减趋势,要将它们都弹出,再加入元素5。
整体就是一个这样的操作。理解了单调栈,单调队列的概念后,再将其应用进题目里,就不会那么懵逼了。
class Solution {
private:
class MyQueue{
public:
deque<int> que;
void pop(int value){
if (!que.empty() && value == que.front()){//这里只有在要弹出的元素为队首元素即最大值时才做弹出,因为不是最大值的在最大值加入的时候就已经被卷走了
que.pop_front();
}
}
void push(int value){
while (!que.empty() && value > que.back()){
que.pop_back();
}
que.push_back(value);
}
int front(){
return que.front();
}
};
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
MyQueue que;
vector<int> result;
for (int i = 0; i < k; i++){
que.push(nums[i]);
}
result.push_back(que.front());
for (int i = k; i < nums.size(); i++){
que.pop(nums[i - k]);
que.push(nums[i]);
result.push_back(que.front());
}
return result;
}
};41. 太平洋大西洋水流问题 题目描述:
有一个 m × n 的矩形岛屿,与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界,而 “大西洋” 处于大陆的右边界和下边界。
这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights , heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。
岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。
返回网格坐标 result 的 2D 列表 ,其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。
示例:
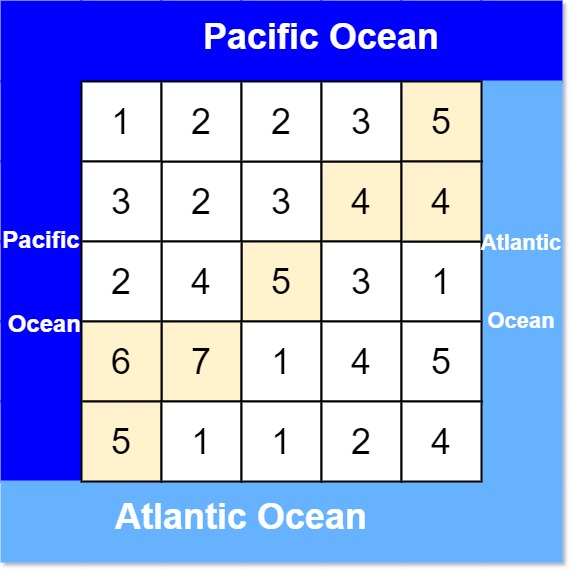
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]] 输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
本题和昨天讲的岛屿问题相差不是太多,都是一个形式里出的题目。
主要还是在寻找遍历的方法,如果按照惯性思维来想,一般都会想先找到最大的区域,再来判断深搜能否到达左上边界和右下边界,就会遍历每个节点来判断其是否能够达到边界。思路直白,但很容易就会超时。
我们可以转变思想,从四周向中间查找比自身高的节点,最终找到最高的点,这个点如果可以从太平洋和大西洋这两个边界都到达,那就说明这个点的雨水可以流到两洋。
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
void dfs(vector<vector<int>>& heights, vector<vector<bool>>& visited, int x, int y){
if (visited[x][y]) return;
visited[x][y] = true;
for (int i = 0; i < 4; i++){
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= heights.size() || nexty < 0 || nexty >= heights[0].size()) continue;
if (heights[x][y] > heights[nextx][nexty]) continue;//自身大于下一节点,即边界节点大于中间节点,这就不是我们要找的高地了
dfs(heights, visited, nextx, nexty);
}
return;
}vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
vector<vector<int>> result;
int n = heights.size();
int m = heights[0].size();
vector<vector<bool>> pacific = vector<vector<bool>>(n, vector<bool>(m, false));
vector<vector<bool>> atlantic = vector<vector<bool>>(n, vector<bool>(m, false));
for (int i = 0; i < n; i++){
dfs(heights, pacific, i, 0);
dfs(heights, atlantic, i, m - 1);
}
for (int j = 0; j < m; j++){
dfs(heights, pacific, 0, j);//深搜中会将能够到达太平洋的点都标记为true
dfs(heights, atlantic, n - 1, j);//深搜中会将能够到达大西洋的点都标记为true
}
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
if (pacific[i][j] && atlantic[i][j]) result.push_back({i, j});在太平洋和大西洋的标记中都为true就说明这个点能够到达两洋
}
}
return result;
}1020.飞地的数量 题目描述:
给你一个大小为 m x n 的二进制矩阵 grid ,其中 0 表示一个海洋单元格、1 表示一个陆地单元格。
一次 移动 是指从一个陆地单元格走到另一个相邻(上、下、左、右)的陆地单元格或跨过 grid 的边界。
返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。
示例:
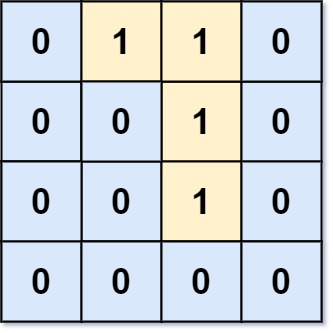
输入:grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]] 输出:0 解释:所有 1 都在边界上或可以到达边界
本题也是和上一题一样,都是昨天遇到的岛屿题目的同一类型,了解之后就不是那么难想了,但还不是很熟悉,代码还是写不太出来。
本题的思路就是现在四周的边界上做深搜,找出与边界相连的大陆,并将其标记为0,再继续在所有的方格中寻找大陆的个数,这是再寻找,找到的大陆个数就是不能到达边界的大陆了。整体相较于上题还是比较简单的。
class Solution {
public:
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
int count;//统计大陆数量
void dfs(vector<vector<int>>& grid, int x, int y){
grid[x][y] = 0;
count++;
for (int i = 0; i < 4; i++){
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
if (grid[nextx][nexty] == 0) continue;
dfs(grid, nextx, nexty);
}
return;
}
int numEnclaves(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
for (int i = 0; i < n; i++){
if (grid[i][0] == 1) dfs(grid, i ,0);//从左边界开始深搜寻找大陆
if (grid[i][m - 1] == 1) dfs(grid, i , m - 1);//从右边界开始深搜寻找大陆
}
for (int j = 0; j < m; j++){
if (grid[0][j] == 1) dfs(grid, 0 , j);//从上边界开始深搜寻找大陆
if (grid[n - 1][j] == 1) dfs(grid, n - 1, j);//从下边界开始深搜寻找大陆
}
count = 0;//清0,接下来才是真正要用到count的时刻
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
if (grid[i][j] == 1) dfs(grid, i ,j);
}
}
return count;
}
};今天本来是因为周六,所以就布置了比较多题目,但实际下来还是花了特别多时间,今天基本没怎么娱乐了,醒了就起来做题,吃饭就看看视频,做题累了就稍微休息一下,基本上所有大块的时间都在学习了。其他的题都还好,就是那个2386找第k大的序列和那题太折磨了,我找的那个题解又不怎么讲清楚,评论还都在说好,我一直看了几十分钟也看不怎么明白,还是评论区有其他大神才把我点明白的,其实一个题解看不明白就应该换一个看看的,但我当时就是犟在那里了,不搞明白就不想走了。挺累的但也不是坚持不下去的那种累,还是挺充实挺有收获的,可能还是对这方面比较感兴趣吧。今天的stm32学习主要做了三个实验,LED灯点亮,LED流水灯,蜂鸣器,点灯大师,已经可以熟练的点灯了😅😅。还是很有意思的,做起来也很开心。以前单片机课上没这么开心的,可能是因为这是自己的单片机,做起来会比较有成就感吧,做完了也可以自己一直留着😋😋😋。
 (LED灯点亮)
(LED灯点亮)
